sector and segment of circle

Circle Sector and Segment

A circular sector or circle sector (symbol: ⌔), is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, the radius of the circle, and is the arc length of the minor sector.
A sector with the central angle of 180° is called a semicircle. Sectors with other central angles are sometimes given special names, these include quadrants (90°), sextants (60°) and octants (45°).
The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle.

n geometry, a circular segment (symbol: ⌓) is an area of a circle informally defined as an area which is "cut off" from the rest of the circle by a secant or a chord. The circle segment constitutes the part between the secant and an arc, excluding of the circle's center.

Contents

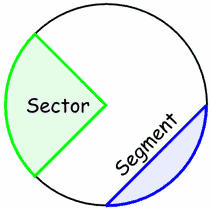
Slices There are two main "slices" of a circle: The "pizza" slice is called a Sector. And the slice made by a chord is called a Segment.

Try Them!

Sector	Segment

Common Sectors

The Quadrant and Semicircle are two special types of Sector: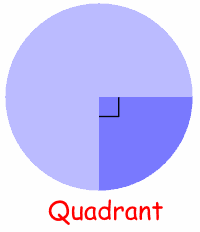

	Quarter of a circle is called a Quadrant. Half a circle is called a Semicircle.

 

Area of a Sector You can work out the Area of a Sector by comparing its angle to the angle of a full circle. Note: I am using radians for the angles.
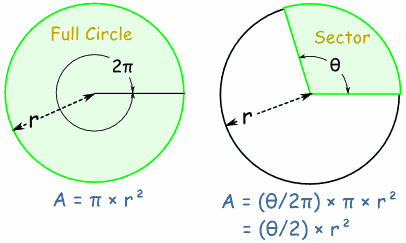This is the reasoning: A circle has an angle of 2π and an Area of: πr2 So a Sector with an angle of θ (instead of 2π) must have an area of: (θ/2π) × πr2 Which can be simplified to: (θ/2) × r2 Area of Sector = ½ × θ × r2   (when θ is in radians) Area of Sector = ½ × (θ × π/180) × r2   (when θ is in degrees)

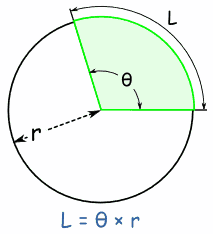Arc Length By the same reasoning, the arc length (of a Sector or Segment) is: L = θ × r   (when θ is in radians) L = (θ × π/180) × r   (when θ is in degrees)

Area of Segment The Area of a Segment is the area of a sector minus the triangular piece (shown in light blue here). There is a lengthy reason, but the result is a slight modification of the Sector formula:
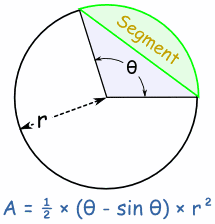Area of Segment = ½ × (θ - sin θ) × r2   (when θ is in radians) Area of Segment = ½ × ( (θ × π/180) - sin θ) × r2   (when θ is in degrees)